I matematici risolvono un importante problema del nastro di Möbius, dopo quasi 50 anni di ricerca

Per quasi cinquant’anni i matematici si sono interrogati su una domanda apparentemente semplice: quanto deve essere piccolo un nastro di Möbius senza intersecarsi?

Ora, Richard Schwartz, un matematico della Brown University, aveva suggerito Una soluzione elegante a questo problema, che era Originariamente Fu proposto dai matematici Charles Weaver e Benjamin Halpern nel 1977.

Nel loro articolo, Halpern e Weaver stabiliscono un limite per i nastri di Möbius basato sulla geometria familiare dei pezzi piegati di carta rigida: il rapporto tra la lunghezza e la larghezza della carta deve essere maggiore di √3, o circa 1,73.

Ad esempio, un nastro di Möbius lungo un centimetro deve essere più largo di √3 ovvero 1,73 centimetri.

Schwartz Lui dice È diventato “dipendente” dal problema della nudità di Möbius dopo averlo scoperto quattro anni fa durante una conversazione con un collega.

Ha avuto diversi tentativi di risolverlo nel corso degli anni e ha pubblicato Carta nel 2021 Con un approccio promettente che alla fine fallì.

Incapace di lasciare il problema da solo, Schwartz ha recentemente iniziato a sperimentare la frantumazione di strisce di Möbius di carta nella speranza che la forma bidimensionale fosse più facile da manipolare matematicamente.

Ma quando ha tagliato obliquamente uno di questi anelli (operazione necessaria per risolvere il problema di ottimizzazione), ha visto qualcosa che non si aspettava.

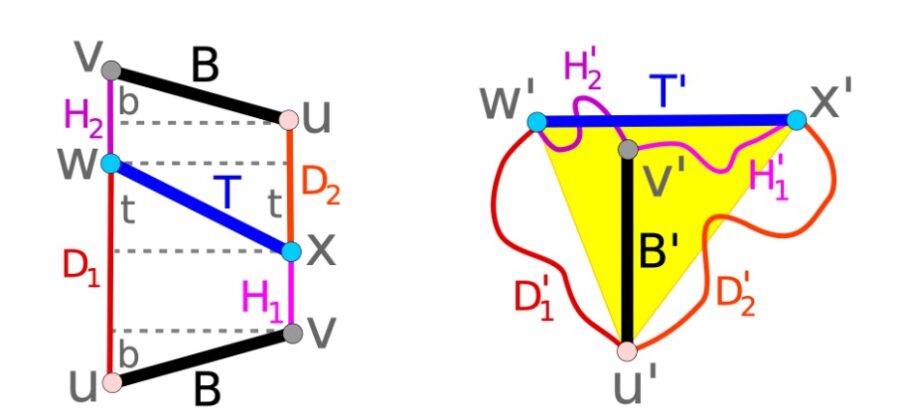
La lunghezza di un foglio di carta 2D non assomiglia ad un parallelogramma, come ha affermato nel suo primo articolo. Ma era un trapezio – Una forma con quattro lati diritti, dove solo due lati sono paralleli tra loro.

“In modo imbarazzante, ho recentemente scoperto di aver commesso un errore nell’impostare il problema di ottimizzazione”, ha detto Schwartz Lui scrive.

Nel corso di tre notti insonni – e con l’aiuto di alcuni colleghi – Schwartz ha corretto il suo errore e… è stato trovato “Un’ottima guida” al passaggio intermedio “che ha reso il lavoro molto più semplice.”

“Sono rimasto stupito e felice di scoprire che quando ho risolto correttamente il problema di ottimizzazione, ho ottenuto… √3 proprio sul mio naso!” Lui Lui scrive.

I nastri di Möbius hanno molte proprietà strane, che li hanno resi oggetto di interesse sin dai loro tempi Descritto nel 1858 Dei matematici tedeschi August Möbius e Johann Listing.

I nastri di Möbius lo sono Non orientabile. Ciò significa che la formica che cammina lungo il nastro di Möbius non si trova mai all’interno, all’esterno, alla parte superiore o inferiore della forma.

Durante i loro viaggi, le formiche coprono entrambi i lati del nastro con un movimento continuo.

Questa è la possibilità di utilizzare entrambi i lati della superficie senza dover capovolgere il nastro Realizza utili strisce di Möbius Per apparecchi di registrazione, macchine da scrivere, nastri trasportatori, cartucce di stampa e montagne russe.

I nastri di Möbius vengono utilizzati nella creazione di gioielli Simbolo universale per il riciclaggio E dentro Logo di Google Drive perchè loro sono Cicli senza fine.

Questo documento è stato reso disponibile come prestampa attraverso arXiv.